Graph few-shot and meta learning
Prevailing methods for graphs require abundant label and edge information for learning, yet many real-world graphs only have a few labels available. This presents a new challenge: how to make accurate predictions in the low-data regimes?
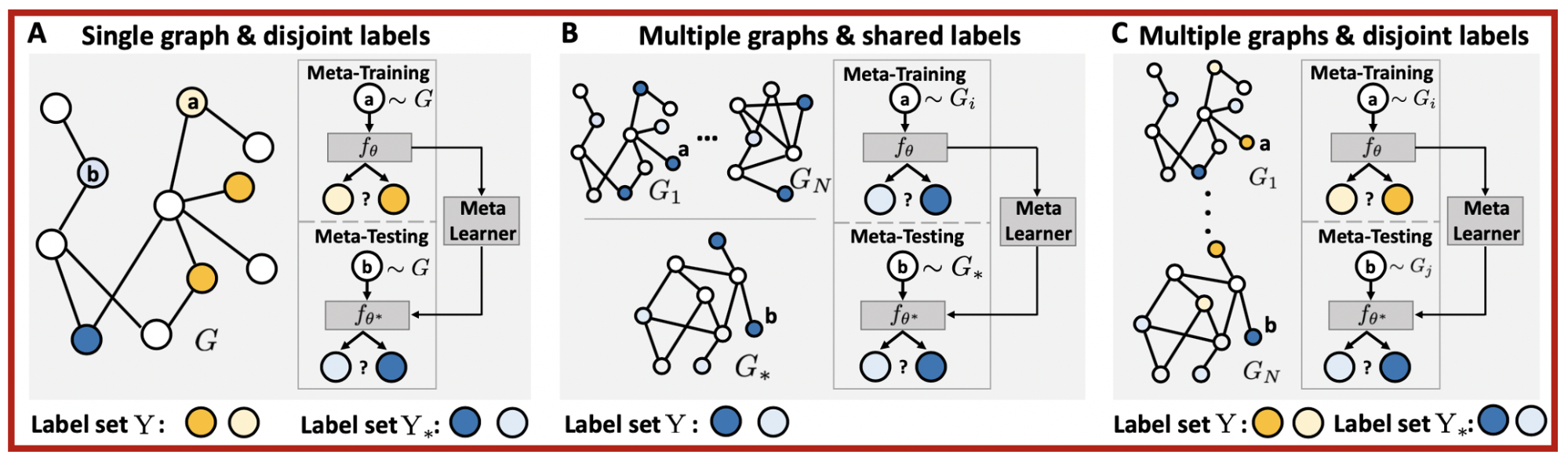
When data for a new task are scarce, meta learning can learn from prior experiences and form much-needed inductive biases for fast adaptation to new tasks. However, a systematic way to formulate meta learning problems on graph-structured data is missing. In this work, we first formulate three important but distinct graph meta learning problems. The main idea is to adapt to the graph or label set of interest by learning from related graphs or label sets.

G-Meta algorithm
G-Meta is a meta learning algorithm that excels at all of the above meta learning problems. In contrast to the status quo that propagate messages through the entire graph, G-Meta uses local subgraphs to transfer subgraph-specific information and learn transferable knowledge faster via meta gradients.
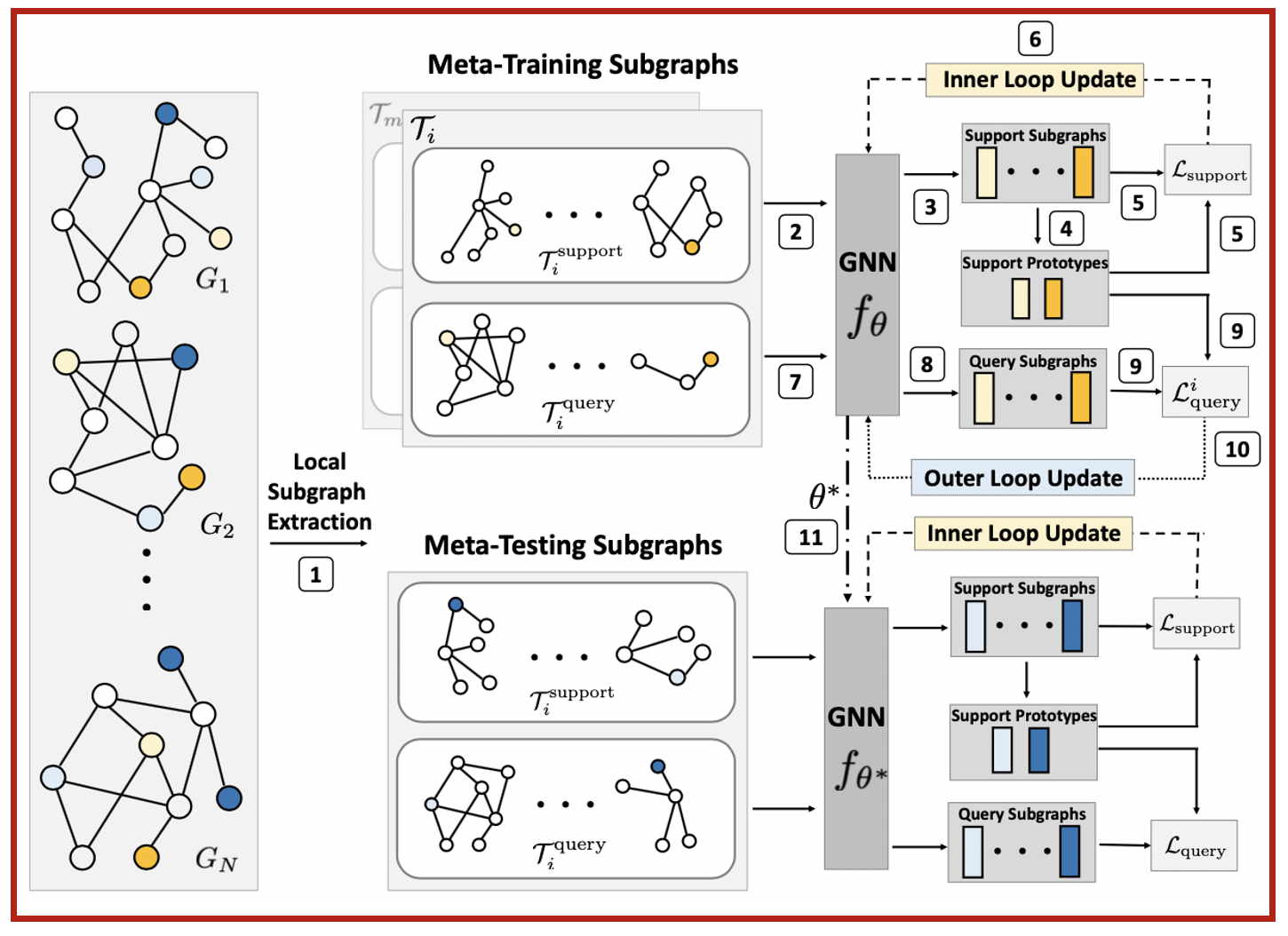
Attractive properties of G-Meta
(1) Theoretically justified: We show theoretically that the evidence for a prediction can be found in the local subgraph surrounding the target node or edge.
(2) Inductive: As the input of GNN is a different subgraph for each propagation during meta-training, it can generalize to never-before-seen subgraphs, such as the ones in the meta-testing. This is in contrast to previous works where inductiveness means using the same weight generated from one single trained graph and applying it to a never-before-seen structurally different graph.
(3) Scalable: In a typical graph meta learning setting, we have many graphs and each have large amounts of nodes and edges. But each task is only looking at a few data points scattered across graphs. Previous works propagate through all of the graphs to generate embeddings for a few nodes, which is wasteful. In contrast, G-Meta simply extracts the small subgraphs around a few data points for every task, and is thus not restricted by any number of nodes, edges, and graphs.
(4) Broadly applicable: G-Meta uses an individual subgraph for each data point and thus breaks the dependency across graphs and labels. While previous works only excel at one of the graph meta learning problems for either node classification or link prediction tasks, G-Meta works for all of the three graph meta learning problems and both node and link prediction tasks.
G-Meta excels at graph meta learning
Empirically, experiments on seven datasets and nine baseline methods show that G-Meta outperforms existing methods by up to 16.3%. Unlike previous methods, G-Meta successfully learns in challenging, few-shot learning settings that require generalization to completely new graphs and never-before-seen labels. Finally, G-Meta scales to large graphs, which we demonstrate on a new Tree-of-Life dataset consisting of 1,840 graphs, a two-orders of magnitude increase in the number of graphs used in prior work.
Publication
Graph Meta Learning via Local Subgraphs
Kexin Huang, Marinka Zitnik
NeurIPS 2020 [arXiv] [poster]
@inproceedings{huangG-Meta2020,
title={Graph Meta Learning via Local Subgraphs},
author={Huang, Kexin and Zitnik, Marinka},
booktitle={Proceedings of Neural Information Processing Systems, NeurIPS},
year={2020}
}
Code
Source code is available in the GitHub repository.
Datasets
ML-ready datasets used in the paper are provided in the HU data repository and, alternatively, the Microsoft repository.