Multivariate time series are prevalent in various domains, including healthcare, space science, cyber security, biology, and finance. Practical issues often exist in collecting sensor measurements that lead to various types of irregularities caused by missing observations, such as saving costs, sensor failures, external forces in physical systems, medical interventions, to name a few.

Prior methods for dealing with irregularly sampled time series involve filling in missing values using interpolation, kernel methods, and probabilistic approaches. However, the absence of observations can be informative on its own, and thus imputing missing observations is not necessarily beneficial. While modern techniques involve recurrent neural network architectures (e.g., RNN, LSTM, GRU) and transformers, they are restricted to regular sampling or assume aligned measurements across modalities. For misaligned measurements, existing methods rely on a two-stage approach that first imputes missing values to produce a regularly-sampled dataset and then optimizes a model of choice for downstream performance. This decoupled approach does not fully exploit informative missingness patterns or deal with irregular sampling, thus producing suboptimal performance. Therefore, recent methods circumvent the imputation stage and directly model irregularly sampled time series.

To address the characteristics of irregularly sampled time series, we propose to model temporal dynamics of sensor dependencies and how those relationships evolve over time. Our intuitive assumption is that the observed sensors can indicate how the unobserved sensors currently behave, further improving the representation learning of irregular multivariate time series. We develop Raindrop, a graph neural network that leverages relational structure to embed and classify irregularly sampled multivariate time series. Raindrop can handle misaligned observations, varying time gaps, arbitrary numbers of observations, and produce multi-scale embeddings via a novel hierarchical attention.

Motivation for Raindrop

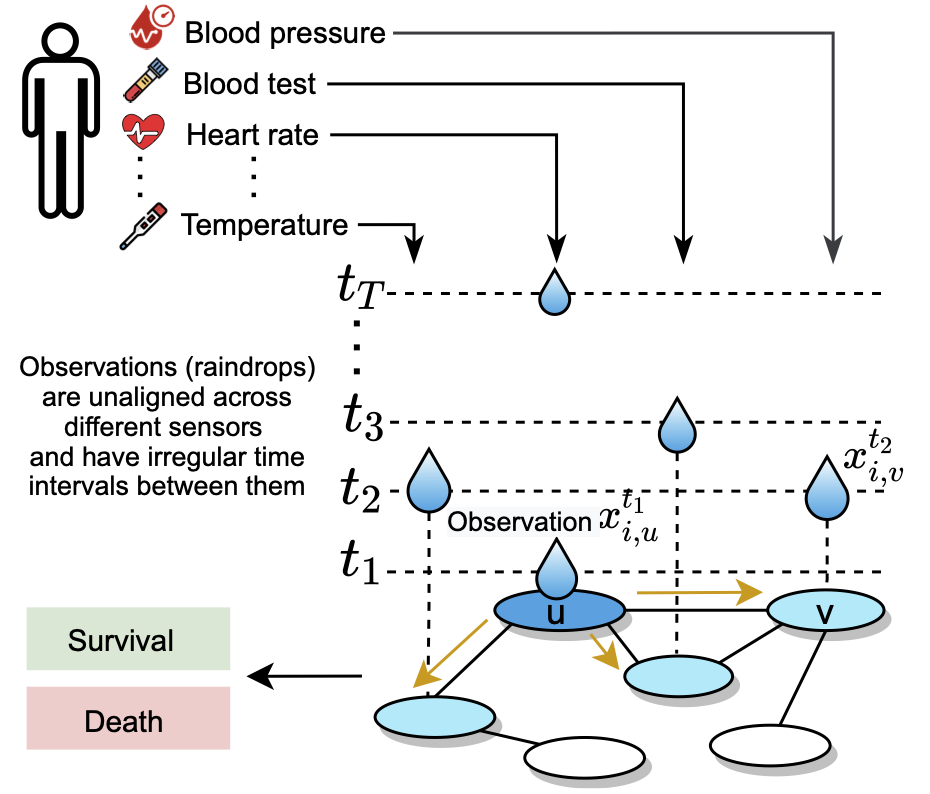
Raindrop takes samples as input, every sample containing multiple sensors and each sensor consisting of irregularly recorded observations (e.g., in clinical data, an individual patient’s state of health is recorded at irregular time intervals with different subsets of sensors observed at different times). Every observation is a real-value scalar (sensor readout).

Raindrop is inspired by how raindrops hit a surface at varying time intervals and create ripple effects that propagate throughout the surface (as shown in the following figure). Mathematically, in Raindrop, observations (i.e., raindrops) hit the sensor graph (i.e., the surface) asynchronously and at irregular time intervals; each observation is processed by passing messages to neighboring sensors (i.e., creating ripples), taking into account the learned sensor dependencies.

The key idea of Raindrop is that the observed sensors can indicate how the unobserved sensors currently behave, which can further improve the representation learning of irregular multivariate time series. Taking advantage of the inter-sensor dependencies and temporal attention, Raindrop leans a fixed-dimensional embedding for irregularly sampled time series.

Raindrop approach

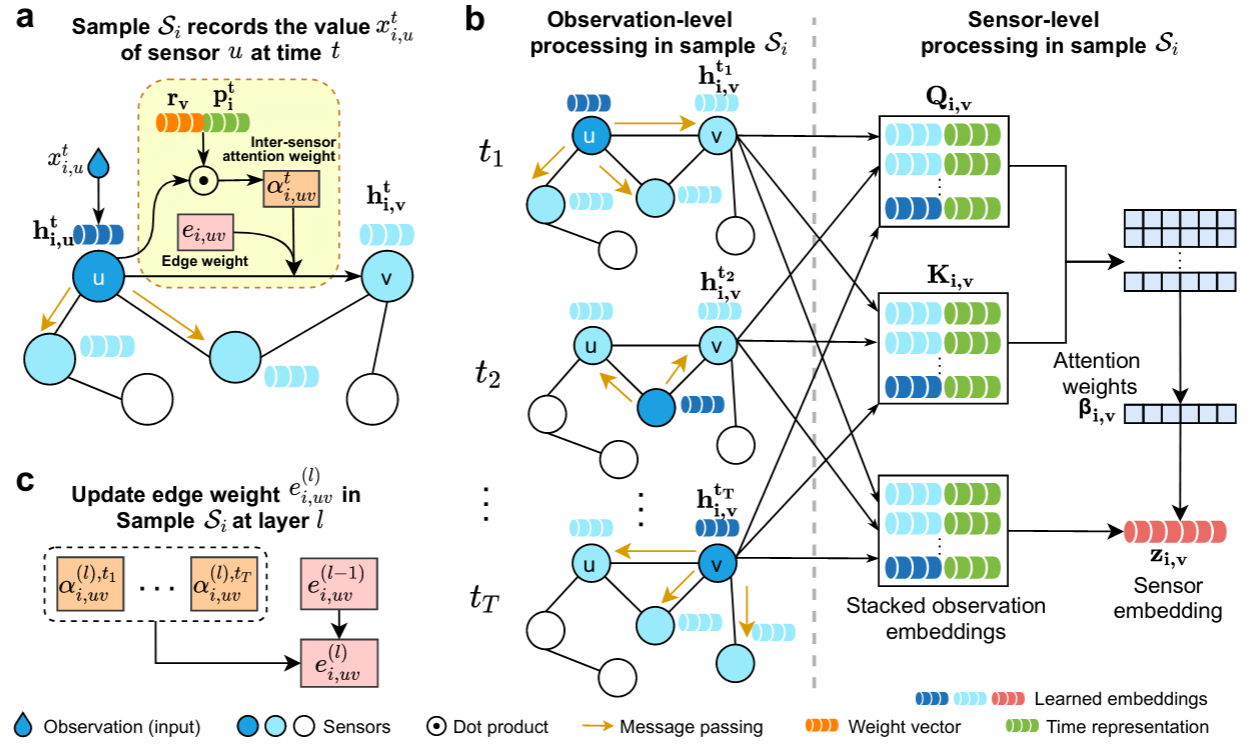
Raindrop learns sample embeddings in a hierarchical architecture that processes individual observations, combines them into sensors, which, in turn, are aggregated to produce sample embeddings:

1. We first construct a graph for each sample where nodes represent sensors and edges indicate relations between sensors.
2. Raindrop generates observation embedding based on observed value, passes messages to neighbor sensors, and generates observation embedding through inter-sensor dependencies (as shown in panel a).
3. We apply the message passing to all timestamps and produce corresponding observation embeddings. We aggregate an arbitrary number of observation embeddings into a fixed-length sensor embedding, while paying distinctive attention to different observations (as shown in panel b) through temporal self-attention. We independently apply the sensor-level processing procedure to all sensors.
4. At last, we use a readout function to merge all sensor embeddings to obtain a sample embedding. The learned sampled embedding can be fed into a downstream task such as classification.

Attractive properties of Raindrop

• Unique capability to model irregularly sampled time series: Raindrop can learn fixed-dimensional embedding for irregularly sampled multivariate time series while addressing challenges including misaligned observations, varying time gaps, and arbitrary numbers of observations.
• Modeling of inter-sensor structure: To the best of our knowledge, Raindrop is the first model adopting neural message passing to model inter-sensor dependencies in irregular time series.
• Excellent performance on leave-sensor-out scenarios: Raindrop outperforms five state-of-the-art methods across three datasets and four experimental settings, including a setup where a subset of sensors in the test set have malfunctioned (i.e., have no readouts at all).

Publication

Graph-Guided Network For Irregularly Sampled Multivariate Time Series
Xiang Zhang, Marko Zeman, Theodoros Tsiligkaridis, and Marinka Zitnik
International Conference on Learning Representations, ICLR 2022

@inproceedings{zhang2022graph,
title = {Graph-Guided Network For Irregularly Sampled Multivariate Time Series},
author = {Zhang, Xiang and Zeman, Marko and Tsiligkaridis, Theodoros and Zitnik, Marinka},
booktitle = {International Conference on Learning Representations, ICLR},
year      = {2022}
}

Code

Pytorch implementation of Raindrop are available in the GitHub repository.

Physical activity monitoring dataset is deposited in the Figshare.

Slides

Slides describing Raindrop are available here.

Authors

• Xiang Zhang
• Marko Zeman
• Theodoros Tsiligkaridis
• Marinka Zitnik