Time series are relevant for many areas, including medical diagnosis and healthcare settings. While representation learning has considerably advanced analysis of time series, learning broadly generalizable representations for time series remains a fundamentally challenging problem. Being able to generate such representations can directly improve pre-training. The central problem is transferring knowledge from a time series dataset to other different datasets during fine-tuning. The difficulty due to distribution shifts and other issues is compounded by the complexity of time series: large variations of temporal dynamics across datasets, varying semantic meaning, system factors, etc.

Supervised pre-training requires large annotated datasets, creating an obstacle to deep learning deployment. For example, in medical domains, experts often disagree on ground-truth labeling, which can introduce unintended biases (e.g., ECG signals falling outside of normal and abnormal rhythms).

We introduce a generalizable concept called Time-Frequency Consistency (TF-C) and use it to develop a broadly generalizable pre-training strategy.

Motivation for TF-C

The TF-C approach uses self-supervised contrastive learning to transfer knowledge across time series domains and pre-train models. The approach builds on the fundamental duality between time and frequency views of time signals. TF-C embeds time-based and frequency-based views learned from the same time series sample such that they are closer to each other in the joint time-frequency space; the embeddings are farther apart if they are associated with different time series samples.

The broad scope of the TF-C principle indicates that the approach promotes positive transfer across different time-series datasets. That is true even when datasets are complex in terms of considerable variations of temporal dynamics across datasets, varying semantic meaning, irregular sampling, and systemic factors.

The following figure gives an overview of the TF-C approach. Given a time series sample, the resulting time and frequency based embeddings are close to each other in a latent time-frequency space (panel a). TF-C expands the scope and applicability of pre-training; it can transfer pre-trained models to diverse scenarios (panel b).

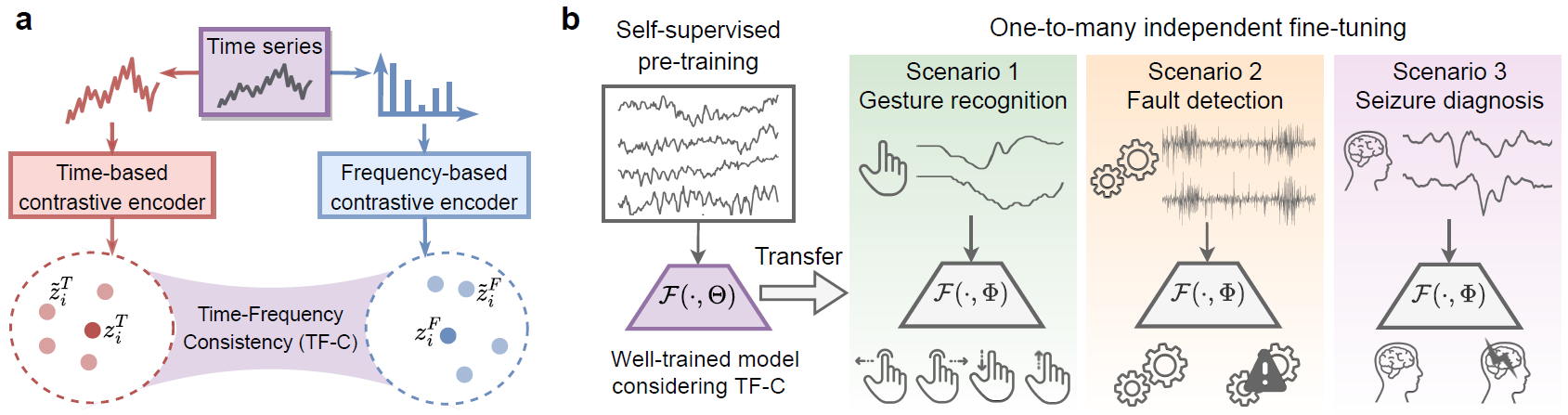
TF-C approach

TF-C has four neural network components (as shown in the following figure):

• Contrastive time encoder,
• Contrastive frequency encoder, and
• two cross-space projectors that map time-based and frequency-based representations to the same time-frequency space.

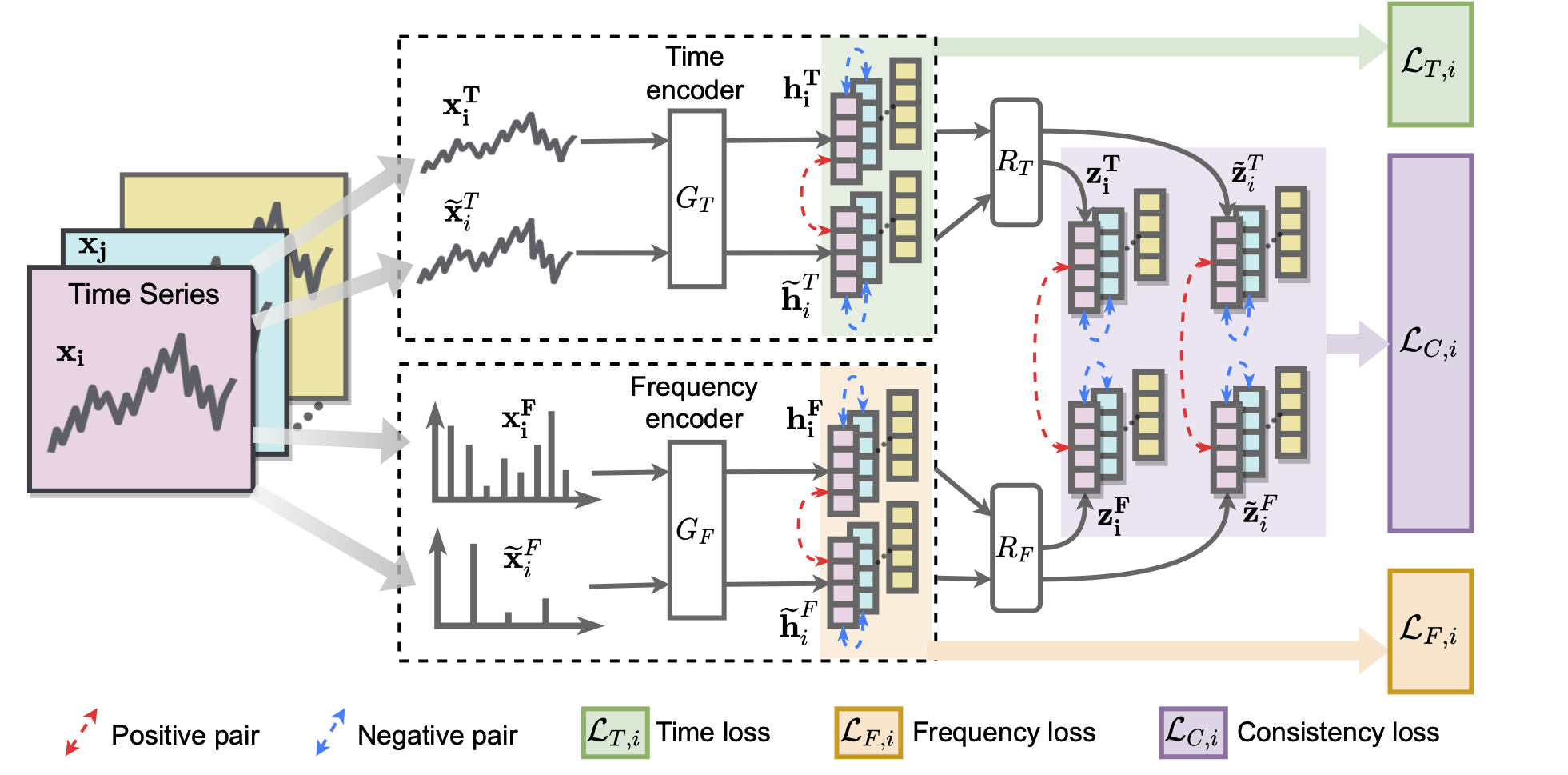
To position time-based and frequency-based embeddings close together, TF-C specifies the following constrastive learning objective:

1. We first apply time-domain augmentations to the input time series sample. The embeddings of the original and the augmented views produced by the time-domain encoder are used to compute a term in the contrastive loss.

2. We transform the input time series to its frequency spectrum. Then, similarly to before, we apply frequency-domain augmentations to the input time series sample, produce the embeddings, and compute another term in the contrastive loss.

3. TF-C requires the consistency between time-domain and frequency-domain representations, which is achieved by a well-designed consistency loss item measured in the time-frequency space. As shown in the figure, our total contrastive loss is a weighted sum of these three terms.

4. Finally, during the fine-tuning phase, we concatenate the time-domain and frequency-domain embeddings to form the sample embedding. This learned sample embedding can be fed into a downstream task such as classification.

Attractive properties of TF-C

• A generalizable assumption (TF-C) for time series: It is grounded in the signal theory that a time series can be represented equivalently in either the time or frequency domain. Hence, our assumption is very reasonable that TF-C is invariant to different time-series datasets and can guide the development of effective pre-training models.

• Self-supervised pretraining for diverse scenarios: The TF-C model can be used with pre-training dataset that are entirely unlabelled. Results show that TF-C provides effective transfer across four scenarios involving time series datasets with different kinds of sensors and measurements and still achieve strong performance when the domain gap is large (e.g., when pre-training and fine-tuning data points are given in different feature spaces or have different semantic meaning).

Publication

Self-Supervised Contrastive Pre-Training For Time Series via Time-Frequency Consistency
Xiang Zhang, Ziyuan Zhao, Theodoros Tsiligkaridis, and Marinka Zitnik
Proceedings of Neural Information Processing Systems, NeurIPS 2022 [arXiv]

@inproceedings{zhang2022self,
title = {Self-Supervised Contrastive Pre-Training For Time Series via Time-Frequency Consistency},
author = {Zhang, Xiang and Zhao, Ziyuan and Tsiligkaridis, Theodoros and Zitnik, Marinka},
booktitle = {Proceedings of Neural Information Processing Systems, NeurIPS},
year      = {2022}
}

Code

PyTorch implementation of TF-C and all datasets are available in the GitHub repository.

Datasets

• SleepEEG dataset of whole-night EEG recordings monitored by a sleep cassette

• Epilepsy dataset of single-channel EEG measurements from 500 subjects

• FD-A dataset of an electromechanical drive system monitoring the condition of rolling bearings

• FD-B dataset of an electromechanical drive system monitoring the condition of rolling bearings

• HAR dataset of human daily activities, including walking, walking upstaris, walking downstairs, sitting, standing, and laying

• Gesture dataset of accelerometer measurements for eight hand gestures

• ECG dataset of ECG measuruments across four underlying conditions of cardiac arrhythmias

• EMG dataset of EMG recordings of muscular dystrophies and neuropathies

Authors

• Xiang Zhang
• Ziyuan Zhao
• Theodoros Tsiligkaridis
• Marinka Zitnik